Spændings-tøjningsforløb

Ligesom ved metallerne har man ved de polymere materialer fornøjelse af at optegne spændings-tøjningsdiagrammer, som også kaldes arbejdslinjer.
Først optegnes kurver over sammenhængen mellem deformationen (fx forlængelsen) af en materialeprøve og den til deformationen nødvendige kraft. Da kraften naturligvis vil være dobbelt så stor, hvis prøve­legemets tværsnitsareal fordobles, omregnes kraften altid til en spænding, dvs. kraften pr. tværsnitsarealenhed. På samme måde om­regnes deformationen til den relative deformation, hvilket vil sige den ak­tuelle deformation i forhold til den aktuelle måleafstand.

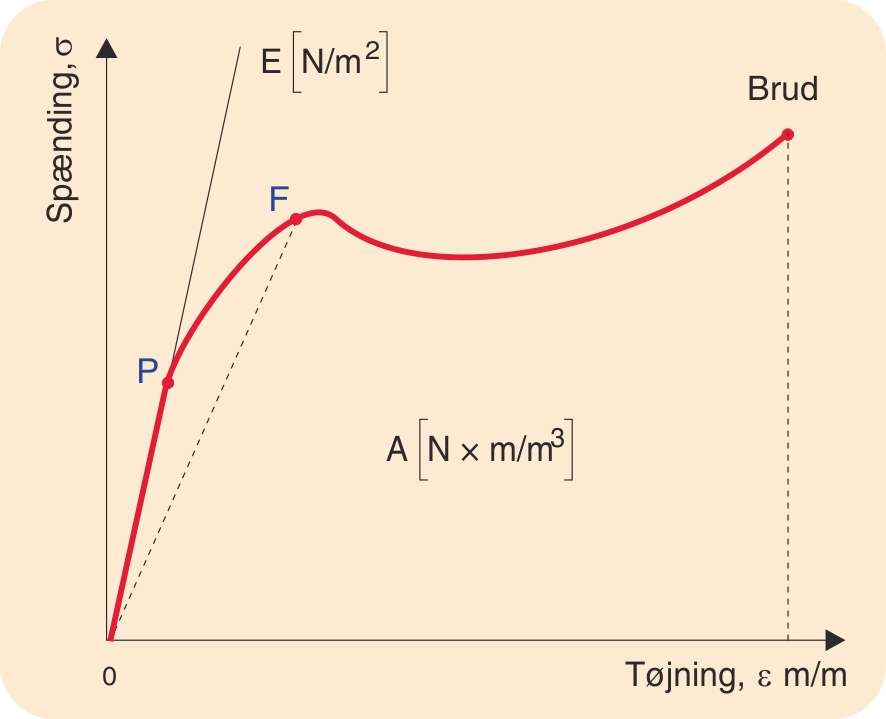
Relativ deformation kaldes tøj­ning. Derved kan man med ret stor tilnærmelse tillade sig at sammenligne arbejdslinjer, der er baseret på forskellige størrelser af prøvelegemer. Nor­malt tænker man for det meste på træk­prøvning, når man taler om spæn­dings-tøjningsdiagrammer, men der fås tilsvarende arbejdslinjer ved alle andre de­formationstil­fælde, det være sig tryk-, bøj­nings-, forskydnings- eller vridningsbelastning.

Kurvens første stykke er ret­linjet, dvs. der er proportionalitet mellem den påtrykte spænding og den deraf følgende relative forlængelse, hvis Hookes lov gælder for det pågældende materiale. Materia­lets elasticitetsmodul, E, kan da beregnes som forholdet mellem spændingen og tøjningen ved at benytte Hookes lov:

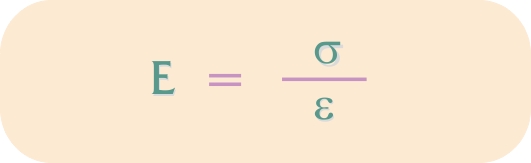
Man kan også sige, at elasticitetsmodulen, E-modulen, er den spæn­ding, som vil medføre 100 %’s tøj­ning, hvis ellers materialet ikke brydes forinden og det var lineært elastisk helt til brud.

Ved spændinger ud over det hookeske område afviger kurven fra den rette linje, dvs. elasticitets­grænsen overskrides. Arealet under arbejdslinjen
(A på figuren nederst på forrige side) er et udtryk for det til deformationen udførte arbejde. Hos termo­plast med delkrystallinsk struktur og hos hærdeplast gælder Hookes lov i det elastiske område, mens det ikke er tilfældet hos amorfe termoplast.

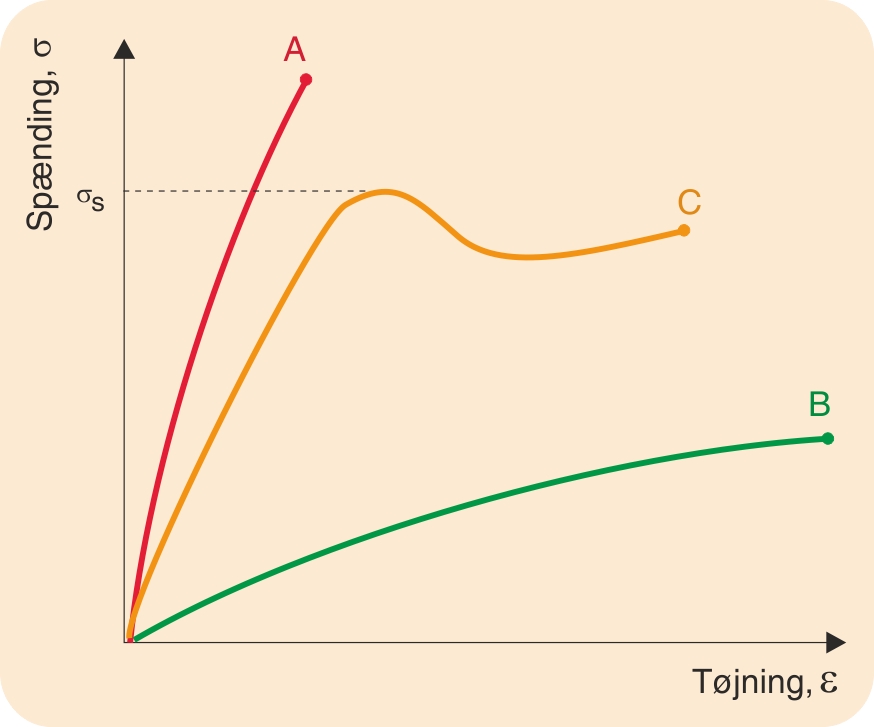
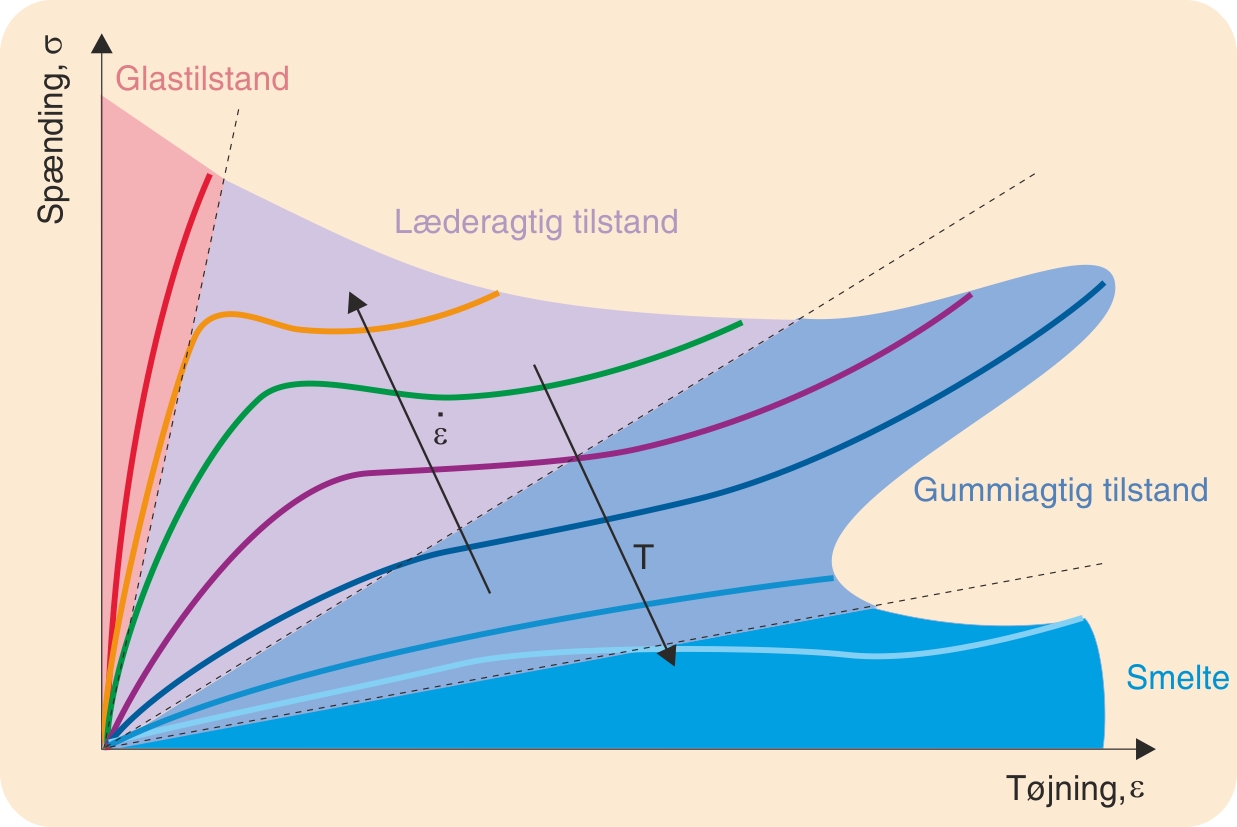
Som det fremgår af det foregående om krybning, har tiden afgørende indflydelse på de polymeres flydeforhold. Derfor vil arbejdslinjer, der optegnes ved forskellige deformationshastigheder, være forskellige. For at få et fuldstændigt billede af en poly­mers flydeforhold må man der­for foretage trækforsøg ved forskellige de­formationshastigheder og om nødvendigt også ved forskellige temperaturer.

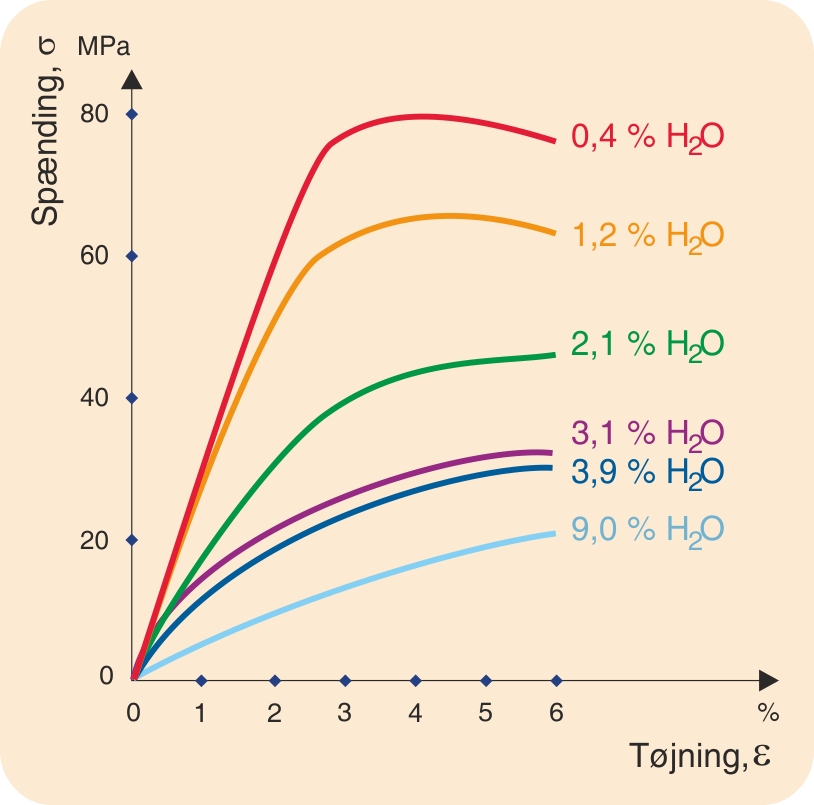
På tilsvarende måde som ved trækprøvning kan man ved trykprøvning og ved bøjeprøvning opnå lignende arbejdslinjer og værdier af brudspænding, elasticitetsmodul og tøjning. Bøjeprøvning kan udføres ved trepunktsbøj­ning og ved firepunktsbøjning, der giver lidt afvigende resultater. Det me­nes, at firepunktsbøjeprøvning giver mest realistiske resultater.
Ved bøjningsbelastning vil reak­tionen i materialet være en kom­bination af træk- og trykspæn­dinger med en principiel fordeling som vist på figurerne nedenfor.

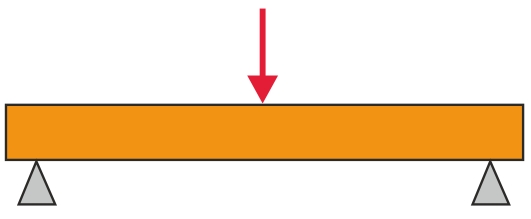
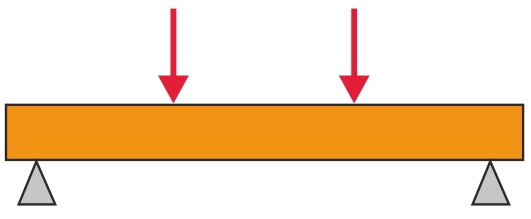
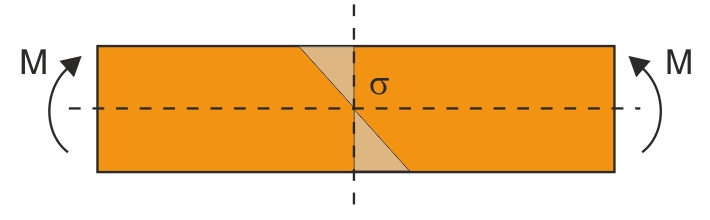
Da polymerer, som tidligere omtalt, udviser udpræget krybning ved længere tids belastning, må man benytte sig af krybedata ved dimensionering af plastemner. Belastes et plast­materiale med konstant last ved konstant temperatur, vil deformationen øges med tiden og give en principiel krybekurve som vist på figuren til nedenfor.

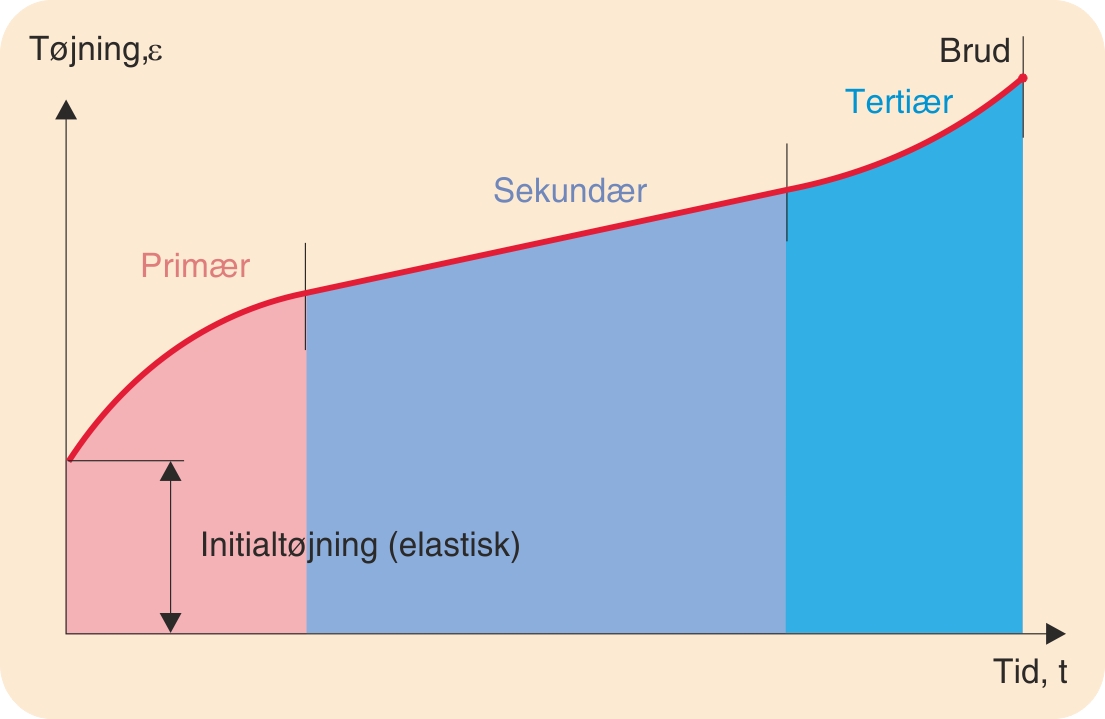
Vi kan genkende de tidligere omtalte tre komponenter, som den totale de­formation er sammensat af.
Den elastiske deformation medfører en øjeblikkelig initial­tøjning. Den visko­elastiske de­formation ses som primær kryb­ning, og den plastiske de­for­ma­tion som det stort set lineære forløb, der benævnes sekun­dær krybning.

For at få brugbare krybedata må man udføre krybeforsøg ved forskellige laster og forskellige temperaturer. Ved at afbilde kurveskarer i samme diagram kan der uddrages en række ingeniørmæssigt inte­ressante data, fx krybemodul, krybebruddata og isokrone spændings-tøjningsforløb.

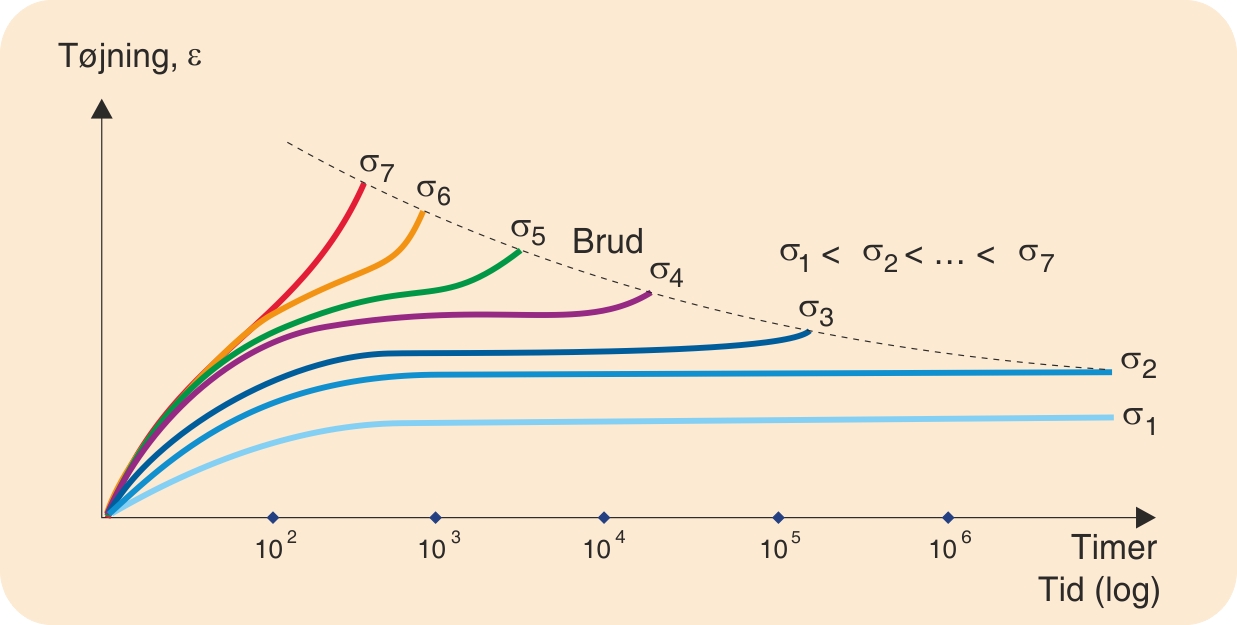
Så­dan et diagram er imidlertid ikke altid operationelt. Derfor konstruerer man ud fra diagrammets oplysninger en række andre diagrammer, som hver for sig har deres fordele, afhængigt af hvilken opgave der skal løses.
Et eksempel er et såkaldt isokront spændings-tøjningsdiagram (iso = samme, kronos = tid), hvor kurverne gælder for forskellige, konstante tider.

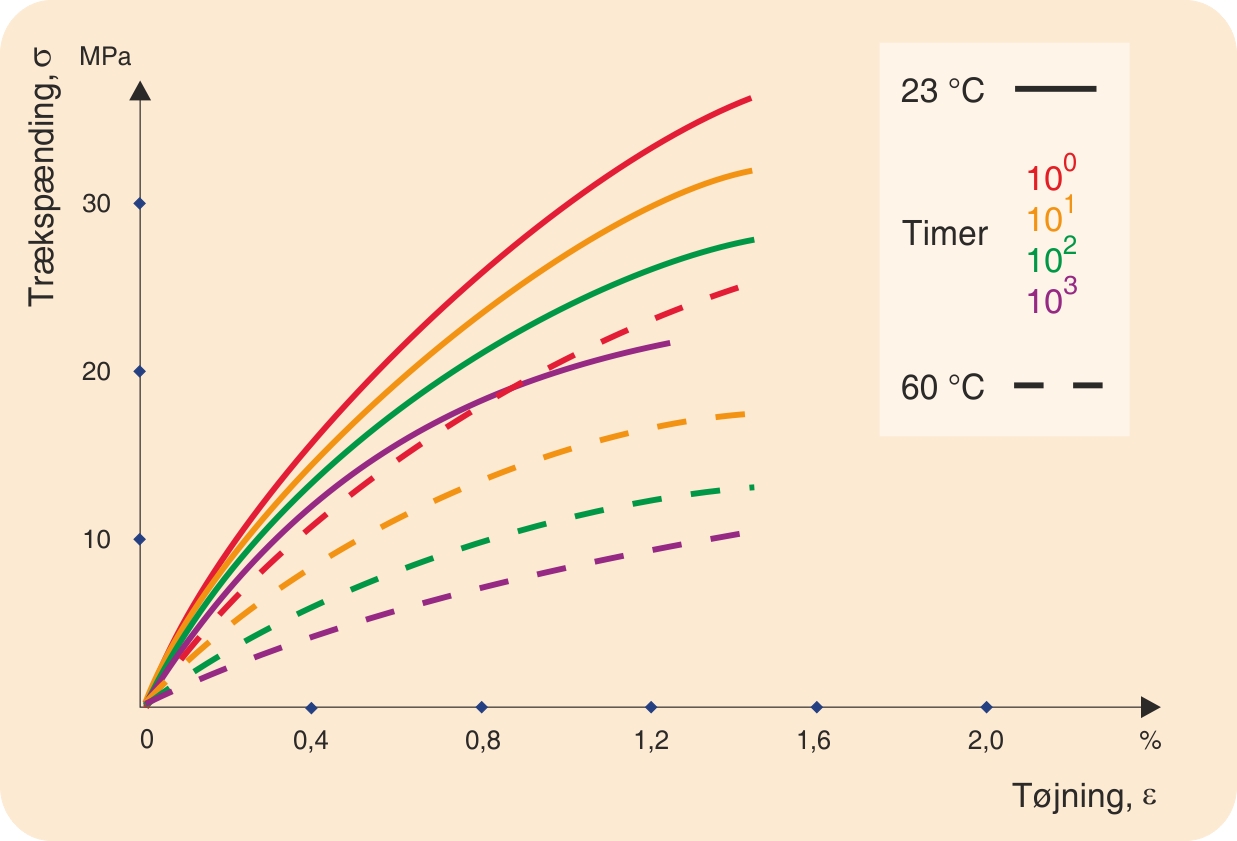
Et andet eksempel er det isometriske spændings-tidsdiagram, hvor det er hensigtsmæssigt at bruge logaritmisk tidsakse. Her er det tøjningen, der holdes konstant på en ræk­ke forskellige værdier.

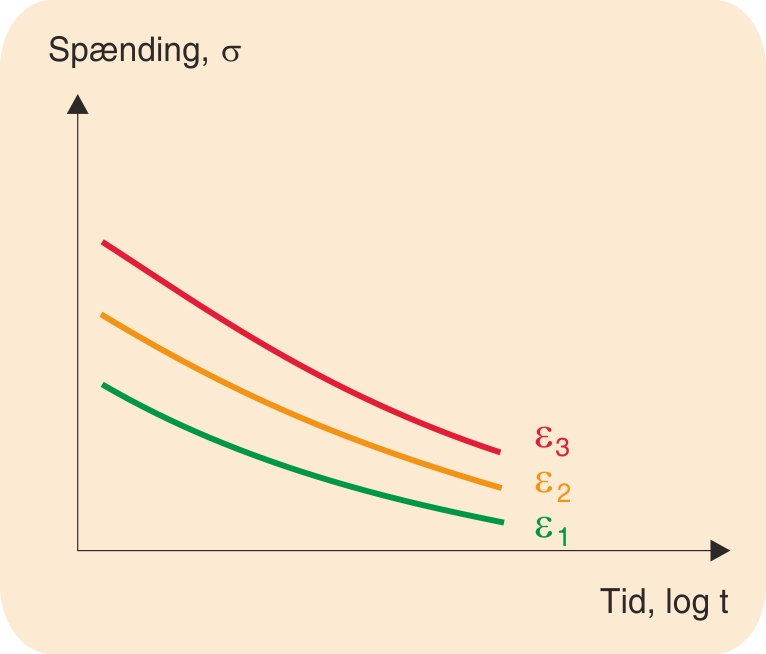
Endelig kan man med fordel afbilde krybemodulets tidsafhængighed ved fastholdt spæn­­ding eller deformation. Også her anvendes en logaritmisk tidsakse.

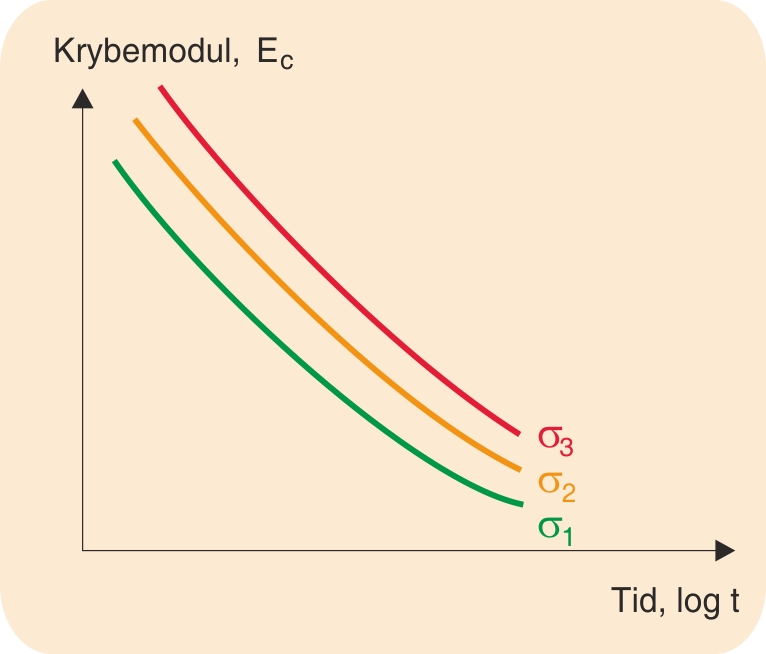
Som tidligere nævnt, vil krybeforholdene påvirkes af eventuel fugtoptagelse, idet der vil indtræde en blød­gø­rende effekt. Desu­den kan der ved efterkrystallisation og dan­­nelse af tværbindinger forekomme sammen­træk­­ning, som kan tilsløre forholdene vedrørende krybning. Endelig vil ældning som følge af på­virkning af ultraviolet lys, oxy­gen og ozon på­virke materialernes krybeegenskaber.